Gaussian process models for stellar variability¶

When fitting exoplanets, we also need to fit for the stellar variability and Gaussian Processes (GPs) are often a good descriptive model for this variation. PyMC3 has support for all sorts of general GP models, but exoplanet interfaces with the celerite2 library to provide support for scalable 1D GPs (take a look at the Getting started tutorial on the celerite2 docs for a crash course) that can work with large datasets. In this tutorial, we go through the process of modeling the light curve of a rotating star observed by Kepler using exoplanet and celerite2.

First, let’s download and plot the data:

[3]:

import numpy as np
import lightkurve as lk
import matplotlib.pyplot as plt

lcf = lk.search_lightcurve(
    "TIC 10863087", mission="TESS", author="SPOC"
).download_all(quality_bitmask="hardest", flux_column="pdcsap_flux")
lc = lcf.stitch().remove_nans().remove_outliers()
lc = lc[:5000]
_, mask = lc.flatten().remove_outliers(sigma=3.0, return_mask=True)
lc = lc[~mask]

x = np.ascontiguousarray(lc.time.value, dtype=np.float64)
y = np.ascontiguousarray(lc.flux, dtype=np.float64)
yerr = np.ascontiguousarray(lc.flux_err, dtype=np.float64)
mu = np.mean(y)
y = (y / mu - 1) * 1e3
yerr = yerr * 1e3 / mu

plt.plot(x, y, "k")
plt.xlim(x.min(), x.max())
plt.xlabel("time [days]")
plt.ylabel("relative flux [ppt]")
_ = plt.title("TIC 10863087")

Warning: 33% (6455/19412) of the cadences will be ignored due to the quality mask (quality_bitmask=8191).

../../_images/tutorials_stellar-variability_4_1.png

A Gaussian process model for stellar variability¶

This looks like the light curve of a rotating star, and it has been shown that it is possible to model this variability by using a quasiperiodic Gaussian process. To start with, let’s get an estimate of the rotation period using the Lomb-Scargle periodogram:

[4]:

import exoplanet as xo

results = xo.estimators.lomb_scargle_estimator(
    x, y, max_peaks=1, min_period=0.1, max_period=2.0, samples_per_peak=50
)

peak = results["peaks"][0]
freq, power = results["periodogram"]
plt.plot(1 / freq, power, "k")
plt.axvline(peak["period"], color="k", lw=4, alpha=0.3)
plt.xlim((1 / freq).min(), (1 / freq).max())
plt.yticks([])
plt.xlabel("period [days]")
_ = plt.ylabel("power")

../../_images/tutorials_stellar-variability_6_0.png

Now, using this initialization, we can set up the GP model in exoplanet and celerite2. We’ll use the RotationTerm kernel that is a mixture of two simple harmonic oscillators with periods separated by a factor of two. As you can see from the periodogram above, this might be a good model for this light curve and I’ve found that it works well in many cases.

[5]:

import pymc3 as pm
import pymc3_ext as pmx
import aesara_theano_fallback.tensor as tt
from celerite2.theano import terms, GaussianProcess

with pm.Model() as model:

    # The mean flux of the time series
    mean = pm.Normal("mean", mu=0.0, sd=10.0)

    # A jitter term describing excess white noise
    log_jitter = pm.Normal("log_jitter", mu=np.log(np.mean(yerr)), sd=2.0)

    # A term to describe the non-periodic variability
    sigma = pm.InverseGamma(
        "sigma", **pmx.estimate_inverse_gamma_parameters(1.0, 5.0)
    )
    rho = pm.InverseGamma(
        "rho", **pmx.estimate_inverse_gamma_parameters(0.5, 2.0)
    )

    # The parameters of the RotationTerm kernel
    sigma_rot = pm.InverseGamma(
        "sigma_rot", **pmx.estimate_inverse_gamma_parameters(1.0, 5.0)
    )
    log_period = pm.Normal("log_period", mu=np.log(peak["period"]), sd=2.0)
    period = pm.Deterministic("period", tt.exp(log_period))
    log_Q0 = pm.Normal("log_Q0", mu=0.0, sd=2.0)
    log_dQ = pm.Normal("log_dQ", mu=0.0, sd=2.0)
    f = pm.Uniform("f", lower=0.1, upper=1.0)

    # Set up the Gaussian Process model
    kernel = terms.SHOTerm(sigma=sigma, rho=rho, Q=1 / 3.0)
    kernel += terms.RotationTerm(
        sigma=sigma_rot,
        period=period,
        Q0=tt.exp(log_Q0),
        dQ=tt.exp(log_dQ),
        f=f,
    )
    gp = GaussianProcess(
        kernel,
        t=x,
        diag=yerr ** 2 + tt.exp(2 * log_jitter),
        mean=mean,
        quiet=True,
    )

    # Compute the Gaussian Process likelihood and add it into the
    # the PyMC3 model as a "potential"
    gp.marginal("gp", observed=y)

    # Compute the mean model prediction for plotting purposes
    pm.Deterministic("pred", gp.predict(y))

    # Optimize to find the maximum a posteriori parameters
    map_soln = pmx.optimize()

optimizing logp for variables: [f, log_dQ, log_Q0, log_period, sigma_rot, rho, sigma, log_jitter, mean]

100.00% [47/47 00:00<00:00 logp = -8.863e+03]

message: Optimization terminated successfully.
logp: -9293.172853145208 -> -8863.135467984936

Now that we have the model set up, let’s plot the maximum a posteriori model prediction.

[6]:

plt.plot(x, y, "k", label="data")
plt.plot(x, map_soln["pred"], color="C1", label="model")
plt.xlim(x.min(), x.max())
plt.legend(fontsize=10)
plt.xlabel("time [days]")
plt.ylabel("relative flux [ppt]")
_ = plt.title("TIC 10863087; map model")

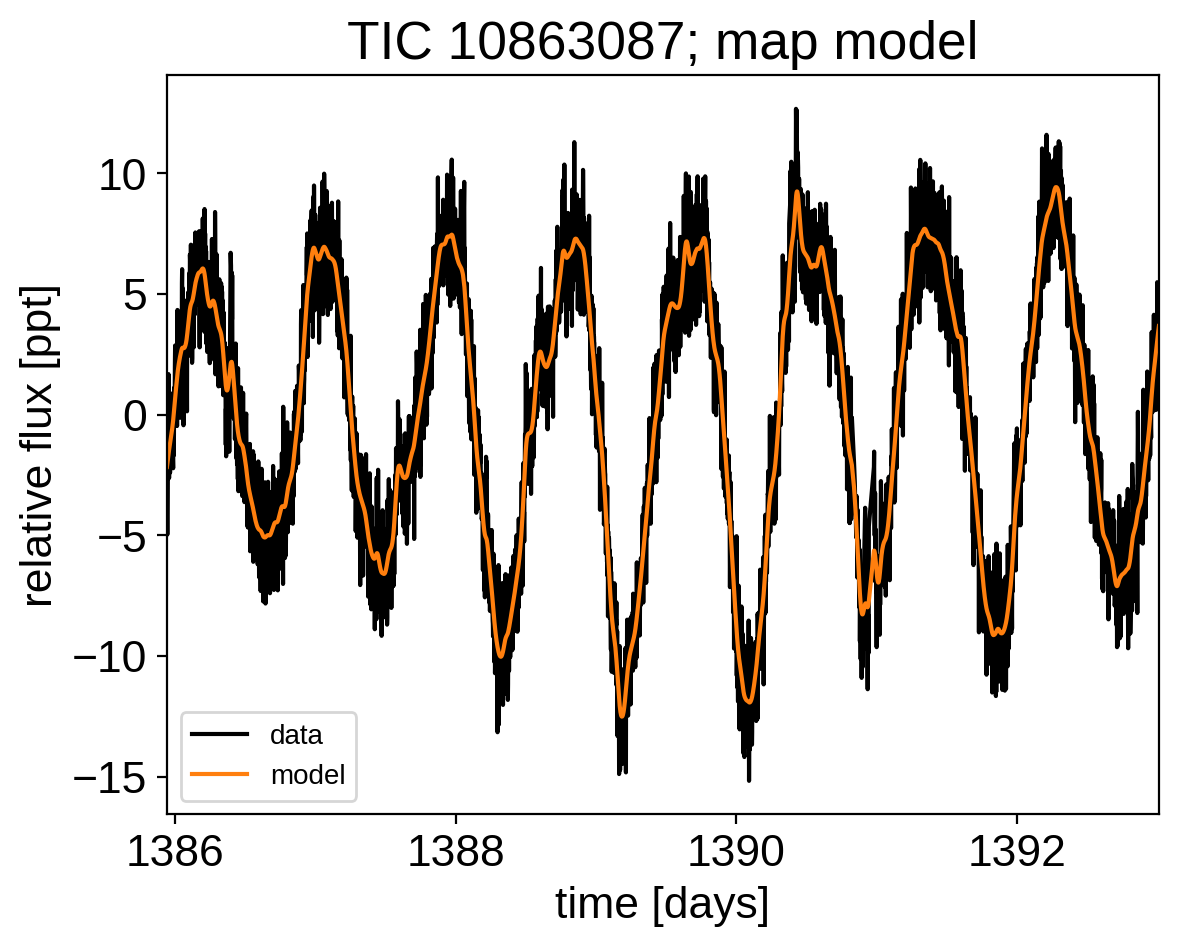
../../_images/tutorials_stellar-variability_10_0.png

That looks pretty good! Now let’s sample from the posterior using the PyMC3 Extras (pymc3-ext) library:

[7]:

np.random.seed(10863087)
with model:
    trace = pmx.sample(
        tune=2500,
        draws=2000,
        start=map_soln,
        cores=2,
        chains=2,
        target_accept=0.95,
        return_inferencedata=True,
    )

Multiprocess sampling (2 chains in 2 jobs)
NUTS: [f, log_dQ, log_Q0, log_period, sigma_rot, rho, sigma, log_jitter, mean]

100.00% [9000/9000 06:24<00:00 Sampling 2 chains, 0 divergences]

Sampling 2 chains for 2_500 tune and 2_000 draw iterations (5_000 + 4_000 draws total) took 386 seconds.

Now we can do the usual convergence checks:

[8]:

import arviz as az

[9]:

az.summary(
    trace,
    var_names=[
        "f",
        "log_dQ",
        "log_Q0",
        "log_period",
        "sigma_rot",
        "rho",
        "sigma",
        "log_jitter",
        "mean",
    ],
)

[9]:

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
f	0.290	0.189	0.100	0.678	0.003	0.002	4201.0	2262.0	1.0
log_dQ	0.732	2.264	-3.185	4.825	0.044	0.033	2666.0	2998.0	1.0
log_Q0	3.732	0.750	2.331	5.237	0.014	0.010	2793.0	1820.0	1.0
log_period	-0.133	0.008	-0.148	-0.118	0.000	0.000	3436.0	2291.0	1.0
sigma_rot	3.145	0.608	2.111	4.259	0.011	0.008	3790.0	2401.0	1.0
rho	0.263	0.035	0.200	0.329	0.001	0.000	3425.0	2224.0	1.0
sigma	1.590	0.186	1.273	1.951	0.003	0.002	3510.0	2792.0	1.0
log_jitter	-1.301	0.488	-1.890	-0.792	0.023	0.017	1333.0	522.0	1.0
mean	-0.045	0.315	-0.667	0.537	0.005	0.005	4233.0	2609.0	1.0

And plot the posterior distribution over rotation period:

[10]:

period_samples = np.asarray(trace.posterior["period"]).flatten()
plt.hist(period_samples, 25, histtype="step", color="k", density=True)
plt.yticks([])
plt.xlabel("rotation period [days]")
_ = plt.ylabel("posterior density")

../../_images/tutorials_stellar-variability_17_0.png

Variational inference¶

One benefit of building our model within PyMC3 is that we can take advantage of the other inference methods provided by PyMC3, like Autodiff Variational Inference. Here we’re finding the Gaussian approximation to the posterior that minimizes the KL divergence:

[11]:

np.random.seed(10863087)
with model:
    approx = pm.fit(
        n=20000,
        method="fullrank_advi",
        obj_optimizer=pm.adagrad(learning_rate=1e-1),
    )
    approx_trace = approx.sample(3000)

approx_period_samples = approx_trace["period"]
plt.hist(
    period_samples, 25, histtype="step", color="k", density=True, label="MCMC"
)
plt.hist(
    approx_period_samples,
    25,
    histtype="step",
    color="C1",
    linestyle="dashed",
    density=True,
    label="VI",
)
plt.legend()
plt.yticks([])
plt.xlabel("rotation period [days]")
_ = plt.ylabel("posterior density")

100.00% [20000/20000 01:29<00:00 Average Loss = 8,869.4]

Finished [100%]: Average Loss = 8,869.4

../../_images/tutorials_stellar-variability_19_2.png

In this case, the periods inferred with both methods are consistent and variational inference was significantly faster.

Citations¶

As described in the citation tutorial, we can use citations.get_citations_for_model to construct an acknowledgement and BibTeX listing that includes the relevant citations for this model.

[12]:

with model:
    txt, bib = xo.citations.get_citations_for_model()
print(txt)

This research made use of \textsf{exoplanet} \citep{exoplanet} and its
dependencies \citep{celerite2:foremanmackey17, celerite2:foremanmackey18,
exoplanet:arviz, exoplanet:pymc3, exoplanet:theano}.

[13]:

print("\n".join(bib.splitlines()[:10]) + "\n...")


@misc{exoplanet,
  author = {Daniel Foreman-Mackey and Arjun Savel and Rodrigo Luger  and
            Eric Agol and Ian Czekala and Adrian Price-Whelan and
            Christina Hedges and Emily Gilbert and Luke Bouma and Tom Barclay
            and Timothy D. Brandt},
   title = {exoplanet-dev/exoplanet v0.5.0},
   month = may,
    year = 2021,
     doi = {10.5281/zenodo.1998447},
...

← Table of Contents Putting it all together →